Cálculos de la relación de transmisión de engranajes planetarios

Traducido al español por Sergio

Una pregunta que me llega a menudo es como calcular engranajes planetarios usando el generador de plantillas para engranajes

Hacer la cuenta de los dientes para los engranajes planetarios realmente no es tan complicado, por lo que al principio pasé de mencionar como hacerlo. Pero al haber recibido numerosas veces la pregunta de como hacerlo, lo voy a explicar.

Por conveniencia, vamos a llamar R,S y P al número de dientes de los engranajes.

RNúmero de dientes en la corona.
SNúmero de dientes en el planeta (engranaje central).
PNúmero de dientes en los engranajes satélite.
La primera condición para que un engranaje planetario funcione es que todos los dientes tengan el mismo módulo, o el mismo paso circular. Esto asegura que los dientes encajan.

La segunda condición es:
    R = 2 × P + S

Es decir, el número de dientes de la corona es igual al número de dientes en el engranaje central más dos veces el número de dientes en los engranajes satélites.

En los engranajes que vemos a la izquierda esto sería 30 = 2 × 9 + 12

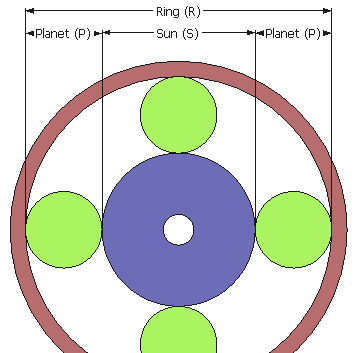Esto se puede ver más claro imaginándonos "engranajes" que solo ruedan (sin dientes) e imaginando un número par de satélites. En la ilustración de la izquierda puedes ver que la suma de los diámetros del engranaje planeta (Sun(S)) más dos engranajes satélite (Planet(P) + Plantet(P)) debe ser igual al tamaño del engranaje corona (Ring(R)).

Ahora imagina que quitamos una de las ruedas satélite verdes y reorganizamos las que quedan para que queden espaciadas a distancias iguales. Seguimos teniendo el mismo tamaño de engranajes.

Ahora imagina que las ruedas tienen dientes. Los dientes sobresaldrán más allá de la línea de la rueda tanto como quedan por debajo de esa línea, de manera que la línea de contacto de los engranajes sería la línea alrededor de los engranajes. La geometría sigue funcionando igual. Si vas al programa generador de engranajes y seleccionas "ver circunferencia primitiva" puedes ver como la circunferencia primitiva es un círculo sobre el que están centrados los dientes.


Aquí vemos otro conjunto de engranajes planetarios. El conjunto interior está sacado...

... y aquí está puesto en su sitio.

En este caso los engranajes satélite tienen 12 dientes, el engranaje planeta tiene 18 y la corona tiene 42 dientes.

Por lo que aplicando

R = 2×P + S

Obtenemos

42 = 2 × 12 + 18

En estas fotos vemos parte de un engranaje planetario de transmisión fascinantemente complicado realizado por Ronald Walters.

Resolviendo relaciones de transmisión de engranajes planetarios

Resolver relaciones de transmisión de un tren de engranajes planetarios puede ser un poco complicado. vamos a usar la siguiente nomenclatura:
TrVelocidad de giro de la corona
TsVelocidad de giro del planeta
TyVelocidad de giro del portasatélites (la pieza con forma de Y en la anterior foto)
RDientes de la corona
SDientes del planeta
PDientes de cada satélite
La relación de transmisión es como sigue:

( R + S ) ×Ty = R × Tr + Ts × S

Ejemplo:

Ahora, en los engranajes planetarios normalmente uno de los engranajes está fijo. Por ejemplo, si mantenemos en una posición fija la corona Tr siempre será cero. Por lo tanto podemos eliminar esos términos de la fórmula anterior y obtenemos:

( R + S ) × Ty = Ts × S

Ahora, si lo que movemos es el engranaje planeta podemos reorganizar la fórmula para resolver la velocidad de giro del portasatélites:

Ty = Ts×
S
R+S
Por lo tanto la relación de transmisión es

  S / (R+S)


Condiciones para el número de dientes y para los satélites

Si quieres que los satélites estén espaciados a distancias iguales y todos engranen en el siguiente diente al mismo tiempo, entonces tu planeta y tu corona, ambos, deben ser exactamente divisibles por el número de satélites (el resultado en ambos casos debe ser un número entero, sin decimales).

Si quieres que todos estén espaciados a distancias iguales, pero no necesitas que todos estén en la misma fase con respecto a sus dientes, entonces el resultado de la suma de los dientes de la corona y los dientes del planeta debe ser divisible exactamente por el número de satélites. Esto es:

( R + S ) es divisible exactamente por el número de satélites.

Sin embargo si no deseas espaciar los satélites a distancias iguales, esta condición no se aplica. Aún así el ángulo entre los engranajes satélites alrededor del planeta está condicionado por:

Ángulop2p =
360
×NDonde N es un número entero.
R+S
Esto quiere decir que el ángulo entre los engranajes satélite es un múltiplo de 360/(R+S).

Finalmente aquí tenemos otro juego de engranajes muy chulo, aunque creo que realmente no es un conjunto de engranajes "planetario".

Si colocas un engranaje dentro de otro, de manera que el piñón interior tiene la mitad de dientes que la corona, cualquier punto de la circunferencia primitiva del piñón interior se moverá adelante y atrás en una línea recta.

La varilla de latón de esta foto se moverá estrictamente de izquierda a derecha en la ranura mientras el piñón es obligado a girar alrededor dentro de la corona. En realidad ese piñón está unido a una manivela que lo mantiene girando alrededor del eje, aunque solamente la parte central de la manivela es visible, por lo que en la foto no parece realmente una manivela.

Créditos de las fotos:
Realmente no he tenido necesidad de construir un conjunto de engranajes planetarios yo mismo, así que usé algunas fotos que me enviaron los lectores.
La primera y última foto fueron tomadas por Brian Kerr
La segunda foto y la tercera me las envió Ronald Walters

Mira también:

Generador de plantillas
de engranajes
Cortando engranajes
de contrachapado
Como hacer engranajes
de madera
Engranaje planetario de transmisión de
Ron Walter
Artilugio agitador de bolígrafos